Einführung

(Hoch et al. 2018, Reinhold, 2018)

Der hier vorgestellte Ansatz zur Vermittlung grundlegender Bruchrechenkonzepte basiert auf dem ALICE-Projekt (Hoch et al., 2018), das an der TUM School of Education durchgeführt wurde und dessen Konzeption, Fragestellungen und Ergebnisse gesammelt in Reinhold (2018) zu finden sind.

Für diesen Ansatz werden Brüche als geometrische Objekte bzw. als Beschreibungen eingeführt, sodass Zähler und Nenner immer konkret und anschaulich interpretiert werden können. Insbesondere beginnen die Beschreibungen immer mit realen Objekten – wie etwa Pizzen, die geteilt werden – um anschließend hauptsächlich mit ikonischen Darstellungen wie Kreis- und Balkendiagrammen zu arbeiten. Die rein symbolische Darstellung von Brüchen als übereinanderstehende Zahlen dient dann nur als Mittel zur Notation.

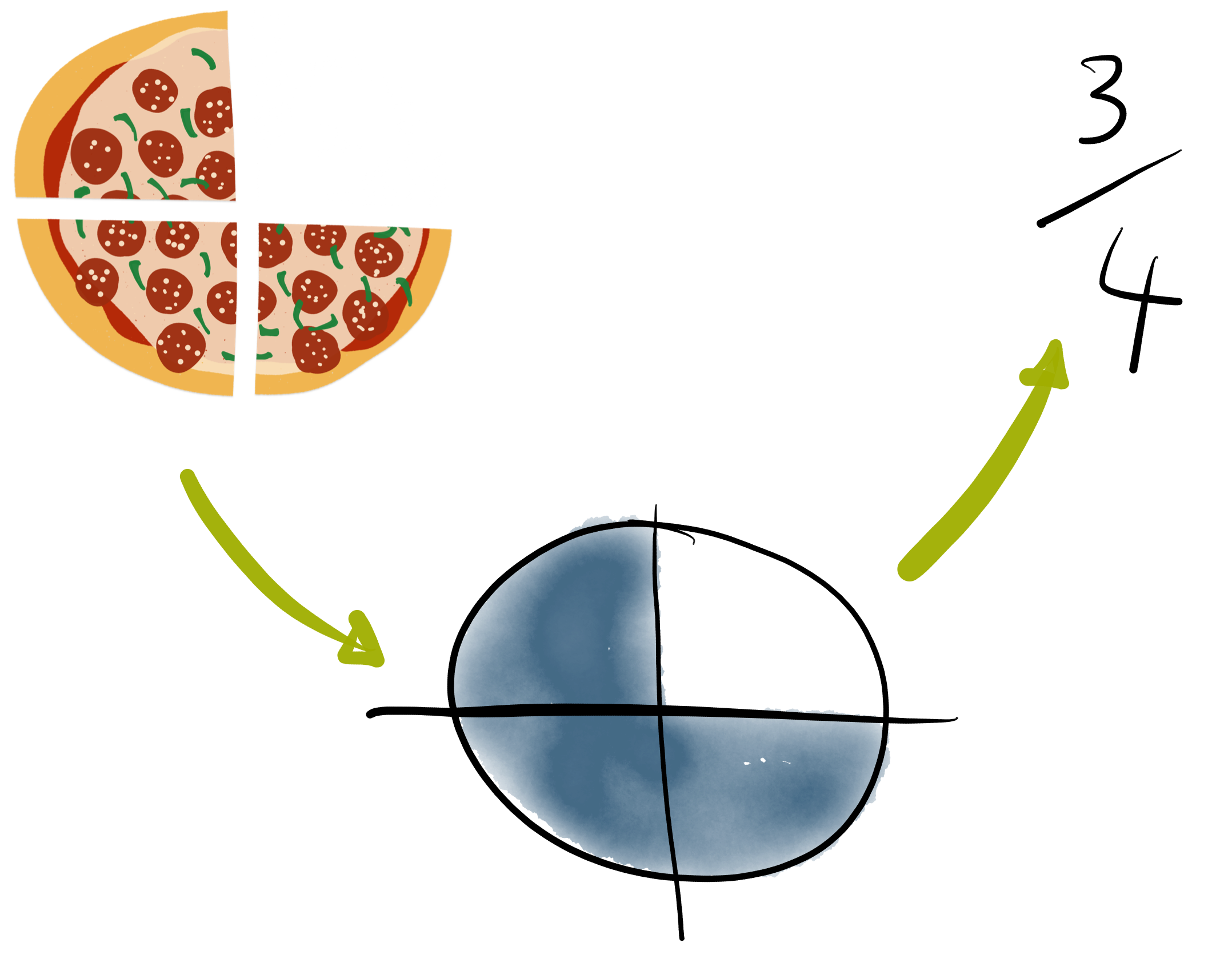
Die ALICE-Studie hat gezeigt, dass Lernende von diesem Ansatz profitieren und weitaus weniger Fehler machen, die auf auswendig gelernten und falsch angewandten formalen Regeln beruhen. Dieser Effekt war in der Studie vor allem bei leistungsstarken Lernenden enorm.

Bei leistungsschwächeren Schülerinnen und Schülern waren die Interaktionsmöglichkeiten mit den geometrischen und realistischen Darstellungen entscheidend für den Lernerfolg: Sich enaktiv mit den Brüchen auseinandersetzen zu können – obwohl die Handlungen zum Teil nur simuliert waren – hat ihnen sehr geholfen, die Bedeutung von Zähler und Nenner besser zu verstehen.

Dieses enaktive Vorgehen kann im Ausschnitt zu Szene 1: Entdecken von wertgleichen Brüchen beobachtet werden: Die Lehrerin erlaubt ihren Schülerinnen und Schülern zunächst, die Aufgabe, $\frac{1}{2}$ auf einem Stück Papier zu markieren, selbst zu lösen und die Ergebnisse zu vergleichen, um so das Thema der Stunde zu entdecken. Erst anschließend geht sie auf die entsprechende Rechenregel ein.

Konkrete Objekte wie etwa Schokoladentafeln tatsächlich zu zerteilen bzw. zu verteilen oder zumindest entsprechende Rechteckdiagramme passend auszumalen, kann im Schulunterricht prinzipiell sehr leicht umgesetzt werden. Allerdings gibt es dabei einige praktische Schwierigkeiten: Soll ein solcher Arbeitsauftrag zu Übungszwecken öfter durchgeführt werden, so muss entsprechend viel Material dafür entweder vorbereitet oder während der Schulstunde erstellt werden. Deswegen bieten sich digitale Lösungen an – wie etwas das eBook, das im ALICE-Projekt verwendet wurde: Unendlich viele Aufgaben können automatisch erstellt werden, geometrische Figuren müssen nicht immer wieder aufs Neue gezeichnet werden und die Aufgaben können sich den Lernenden in ihrem Schwierigkeitsgrad anpassen. Allerdings sei darauf hingewiesen, dass die Vorteile eines solchen digitalen Schulbuchs nichts mit der Art und Weise zu tun haben, wie Brüche und Bruchzahlen tatsächlich vermittelt werden.

Im Folgenden liegt der Fokus auf gewöhnlichen Brüchen. Dezimalbrüche werden hier außen vor gelassen, da diese den Rahmen des Moduls sprengen würden. Außerdem beschränkt sich das Modul auf einige zentrale Aspekte und Konzepte der Bruchrechnung. Themen wie der Zahlenstrahl sind zwar wichtig, lassen sich aber nicht so gut mit dem oben beschriebenen geometrischen Ansatz erläutern.

Die Webversion des eBooks, das im ALICE-Projekt entwickelt wurde, können Sie unter folgendem Link finden: https://www.alice.edu.tum.de/