Sinus
In Szene 1: Einführung und graphische Ableitung mittels digitaler Medien - Teil 1 leitet die Lehrerin gemeinsam mit den Lernenden den Sinus Schritt für Schritt graphisch ab. Dazu wiederholt sie zuerst, wie an das Thema Ableiten herangegangen werden kann.
In Szene 1: Einführung und graphische Ableitung mittels digitaler Medien - Teil 2 wird die Ableitung der Sinusfunktion an markanten Punkten bestimmt.
Die in Szene 1: Einführung und graphische Ableitung mittels digitaler Medien genutzte interaktive Visualisierung kann hier nochmals selbst getestet werden:
Anleitung: Den Punkt auf dem Graphen der Funktion mittles des Schiebereglers verschieben. Mit den Knöpfen die Tangente am Punkt aktivieren und Ableitungswerte in der Tabelle hinzufügen. Nur Kleinbuchstaben in Abhängigkeit von $x$ eingeben. Das Mal-Zeichen wird mittels * eingefügt.
Durch die graphische Ableitung lässt sich allerdings nur die Vermutung aufstellen, dass
\[\sin’(x)=\cos(x)\]
gilt. Die Vermutung lässt sich im Folgenden bestätigen.
Ableitung mittels der h-Methode
Für die Ableitung werden die Additionstheoreme als bekannt vorausgesetzt. Zudem wird noch ein Hilfssatz benötigt:
\[\lim_{x\to 0}\frac{\sin(x)}{x}=1\tag{$*$}\]
und
\[\lim_{x\to 0}\frac{\cos(x)-1}{x}=0\]
Diese sind leicht zu beweisen, wenn die Reihendarstellung der Funktionen bekannt ist und eingesetzt wird. Hier wird ein geometrischer Beweis skizziert:
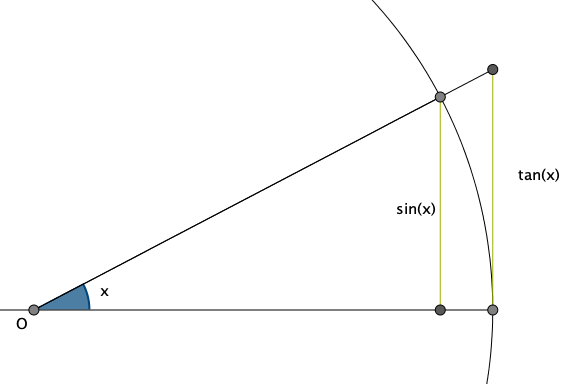
Am Einheitskreis ist zu erkennen, dass für alle $0< x < \frac{\pi}{2}$ gilt, dass
\[\sin(x) < x < \tan(x).\]
Diese Gleichung dividiert durch $\sin(x)$ ergibt
\[1 <\frac{x}{\sin(x)} < \frac{1}{\cos(x)}\]
und die rechte Seite geht für $x\to 0$ klar gegen $1$. Der zweite Teil der Aussage lässt sich analog zeigen.
Angenommen, dass obiges Lemma als bewiesen gilt, kann damit die Ableitung des Sinus und des Cosinus bestimmt werden. Es gilt:
\[\frac{d}{dx}\sin(x)\]
\[=\lim_{h\to 0}\frac{\sin(x+h)-\sin(x)}{h}\]
\[\overset {\text{Additionstheoreme}}{=} \lim_{h\to 0} \frac {\sin(x)\cos(h)+\cos(x)\sin(h)-\sin(x)}{h}\]
\[=\lim_{h \to 0} \left(\sin(x) \frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h} \right)\]
\[\overset{(*)}{=} \sin(x) \cdot 0+\cos(x) \cdot 1\]
\[=\cos(x)\]
Zu beachten ist hier, dass die Additionstheorem nur deswegen verwendet werden konnte, weil die Ableitung über die h-Methode berechnet wurde. Der Beweis für die Ableitung des Cosinus erfolgt analog.
Weitere Informationen zu den trigonometrischen Funktionen finden sie in (Korntreff, 2017).