Multiplikation & Division
Multiplikation
Die Erklärung der Multiplikation von Brüchen lässt sich in drei Schritte gliedern:
- Das Multiplizieren eines Bruches mit einer ganzen Zahl.
- Die Division eines Bruches durch eine ganze Zahl.
- Das Erkennen, dass sich die Multiplikation von Brüchen als Kombination dieser beiden Schritte beschreiben lässt.
Im ersten Schritt wird ein Bruch mit einer ganzen Zahl multipliziert. Dies kann vollständig mit der Vorstellung von Brüchen als Einheiten erklärt werden. Genauso wie $5\,\text{€} \cdot 3= 15\,\text{€}$ ergeben,

so ergeben $\frac{5}{7} \cdot 3 = \frac{15}{7}$. Stücke einer bestimmten Größe werden vervielfacht.

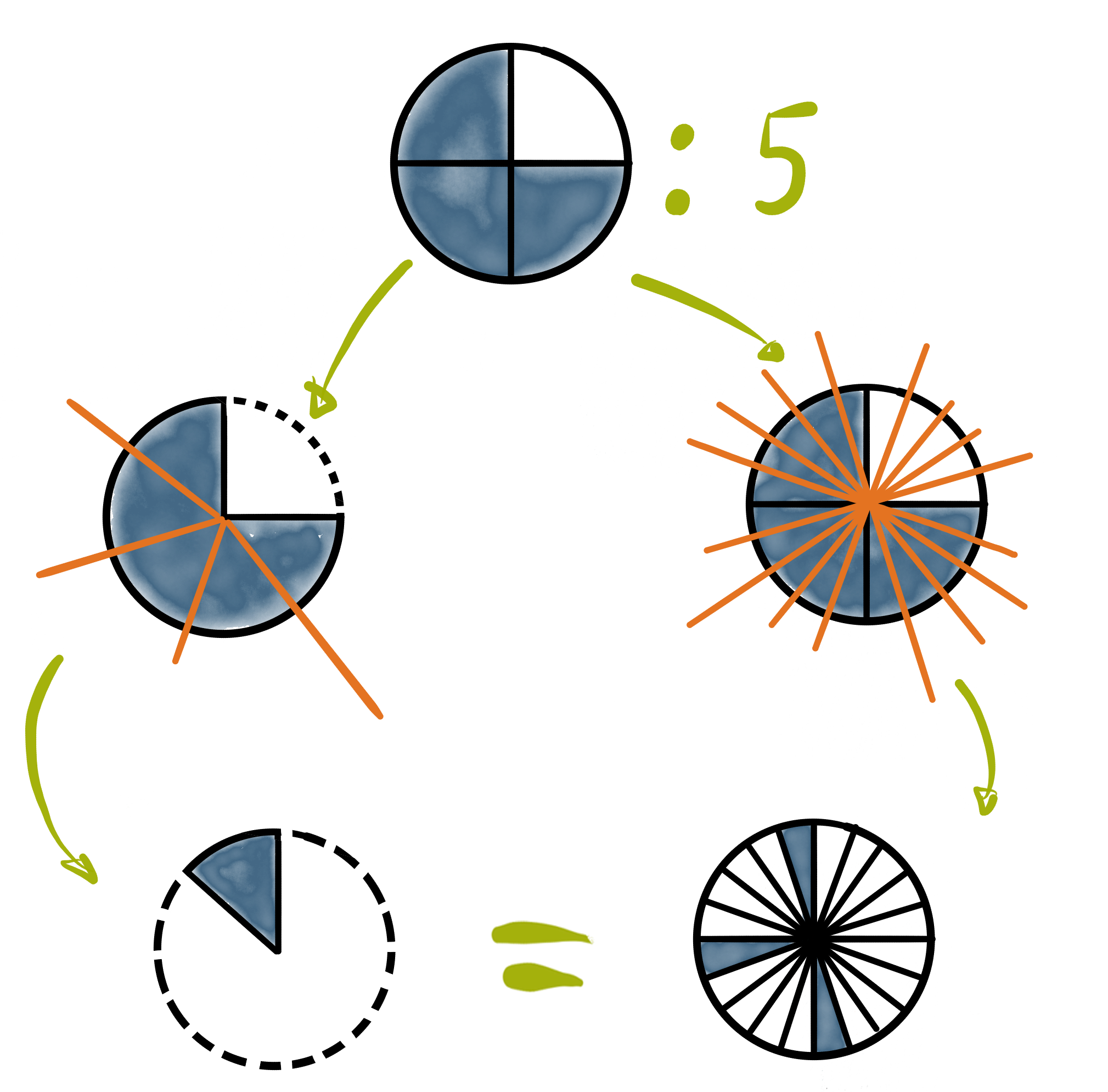
Im zweiten Schritt wird ein Bruch durch eine natürliche Zahl geteilt. Dies funktioniert am einfachsten, wenn der Bruch selbst als Ganzes betrachtet wird und die grundlegende Interpretation von Brüchen erneut herangezogen wird. Wird eine dreiviertel Pizza auf fünf Leute aufgeteilt, $\frac{3}{4} : 5$, so muss sie als Ganzes gefünftelt werden. Dafür kann aber auch ein Fünftel eines jeden Stück der Pizza genommen werden.
Im letzten Schritt können Brüche miteinander multipliziert werden, indem erneut die Interpretation als Teil eines Ganzen oder Teil mehrerer Ganzer herangezogen wird:
\[\frac{2}{3}\cdot \frac{5}{7}\enspace =\enspace \frac{2}{3} \cdot 5 : 7\enspace =\enspace \frac{2}{3} : 7 \cdot 5\enspace =\enspace \frac{14}{15}\]
Wie schon bei der Addition oben ist die Formel $\frac{a}{b}\cdot\frac{c}{d} = \frac{ac}{bd}$ nur eine Folge der Geometrie und nicht das Wesen der Operation.
Division
Die Division von Brüchen ist die konzeptionell komplizierteste arithmetische Operation und vermutlich das schwierigste Unterthema der Bruchrechnung. Sich zu fragen “Wie oft passt es hinein?” kann hier zwar an sich von den natürlichen Zahlen übernommen werden, allerdings sind die Ergebnisse einer Bruchdivision oft nicht offensichtlich. Es bietet sich deshalb an, mit explorativen Aufgaben wie der folgenden bei den Lernenden ein Gespür für diese Ergebnisse zu wecken.
Anleitung: Wählen Sie ausreichend Gläser aus, um den gesamten Saft auszuschenken. Zum Anzeigen einer neuen Aufgabe klicken Sie auf den blauen “Neu”-Knopf.
Die Einführung der Division geht nun genauso wie die der Multiplikation vonstatten und beginnt mit der Frage, wie ein Bruch durch eine natürliche Zahl geteilt werden kann. Ist der Zähler ein Vielfaches des Divisors, so kann dieser direkt geteilt werden. Die Aufgabe z. B. $\frac{8}{9}$ durch $4$ zu teilen, lässt sich umformulieren zu der Frage
Ist der Zähler kein Vielfaches des Divisors, z. B. bei $\frac{8}{9} : 5$, so kann auf zwei Arten vermittelt werden, was zu tun ist.
Einerseits ist eine anschauliche Erklärung möglich. Das Ganze wird erst in $9$ geteilt und soll anschließend noch einmal durch $5$ geteilt werden. Es entstehen $9\cdot 5$ Teile, von denen $8$ genommen werden.

Andererseits kann auch arithmetisch argumentiert werden. Zum Zeitpunkt dieses Themas im Unterrichtsverlauf haben die Lernenden bereits ein (idealerweise sehr gutes) Verständnis dafür, wie wertgleiche Brüche funktionieren. Wenn es also ein Problem ist, dass der Zähler kein Vielfaches des Divisors ist, kann ein wertgleicher Bruch gefunden werden, bei dem das doch der Fall ist. Dies geschieht durch Multiplikation von Zähler und Nenner mit dem Divisor und anschließend kann der neue Zähler einfach geteilt werden. Beide Argumente führen zu der bekannten Regel
Allerdings steht diese hier somit nicht ohne Begründung beziehungsweise Kontext da, was zu Verwirrung führen würde. In der ersten, anschaulichen Erklärung wird (wie schon zuvor bei allen anderen Themen) ein geometrischer Grund geliefert, warum diese Regel sinnvoll ist. Die zweite, arithmetische Erklärung zeigt diese Regel als Ergebnis eines zweistufigen Prozesses,
\[\frac{a}{b} : n\enspace =\enspace \frac{an}{bn} : n\enspace =\enspace \frac{a}{bn},\] dessen erster Schritt bekannt ist und dessen zweiter Schritt eben erklärt wurde. Insbesondere können beide Gedankengänge leicht reproduziert
werden, sollten die Lernenden die fertige Regel einmal vergessen.
Auf ähnliche Weise kann nun auch die Division eines Bruches durch einen Stammbruch erklärt werden. Sind Nenner des Dividenden und des Divisors gleich, so kann wie oben über Pizzastücke argumentiert werden: Soll $\frac{8}{9}$ durch $\frac{1}{9}$ geteilt werden, ist das äquivalent zur Frage
Problematisch ist hier nun der etwas kompliziertere Fall, wenn der Nenner des Dividenden ein Vielfaches des Nenners des Divisors ist; also z. B. bei $\frac{7}{10} : \frac{1}{5}$. Hier können die Stücke des Dividenden zuerst so zusammengefasst werden, dass Fünftel entstehen.

In diesem Beispiel sind das $3\frac{1}{2} = \frac{7}{2}$ Fünftel. Anschließend kann mit derselben Frage wie oben – “Wie viele einzelne Fünftel passen hier rein?” – nun das Ergebnis
\[\frac{7}{10}:\frac{1}{5}\enspace =\enspace \frac{7}{2}\cdot\frac{1}{5}:\frac{1}{5}\enspace =\enspace \frac{7}{2}\] erreicht werden.
Abschließend kann der allgemeine Fall eines Bruches geteilt durch einen Stammbruch analog zum arithmetischen Argument oben behandelt werden. Zu jedem Bruch gibt es einen wertgleichen Bruch, sodass dessen Nenner ein Vielfaches des Nenners des gegebenen Divisors ist. Die komplizierte und abstrakte Regel
wird wieder durch die zwei Stufen
\[\frac{a}{b}:\frac{1}{n}\enspace =\enspace \frac{an}{bn}:\frac{1}{n}\enspace =\enspace \frac{an}{b}\] ersetzt, die für sich genommen bekannt bzw. jetzt anschaulich sind.
Die allgemeine Form der Division setzt sich nun aus der Division durch eine natürliche Zahl und aus der Division durch einen Stammbruch zusammen:
\[\frac{a}{b}:\frac{c}{d}\]
\[ =\enspace \left(\frac{a}{b} : c\right) : \frac{1}{d}\]
\[ =\enspace \frac{a}{bc} : \frac{1}{d} =\enspace \frac{ad}{bc}\]Hier ist nun die Regel
deutlich einfacher zu handhaben als die Folge an Zwischenschritten. Allerdings ist diese Regel nun vollständig anschaulich erklärt. Und auch wenn es insgesamt ein mühseliger und aufwendiger Prozess ist, diese Regel so herzuleiten, lohnt es sich, da die Lernenden dadurch zumindest wissen, dass es einen vernünftigen Grund für die Regel gibt; selbst wenn sie ihn während des Arbeitens nicht immer im Kopf haben.