Einführung am rechtwinkligen Dreieck
In der 9. Jahrgangsstufe des Gymnasiums werden Sinus und Cosinus über rechtwinklige Dreiecke eingeführt. Hierzu müssen die Begriffe, die im Zusammenhang mit rechtwinkligen Dreiecken aufgetaucht sind, wiederholt werden.
Hypotenuse, Ankathete & Gegenkathete
Gegenüber vom rechten Winkel befindet sich stets die längste Seite, die Hypotenuse. Die beiden am rechten Winkel anliegenden Seiten heißen Katheten. Neben dem $90^\circ$ Winkel gibt es noch Winkel $\alpha$ und $\beta$. Betrachten wir zum Beispiel $\alpha$, so liegt direkt an diesem Winkel die Hypotenuse und eine Kathete an. Die anliegende Kathete bezeichnet man als Ankathete von $\alpha$. Die gegenüberliegende Kathete heißt folglich Gegenkathete. Für den Winkel $\beta$ finden wir die An- und Gegenkathete analog.
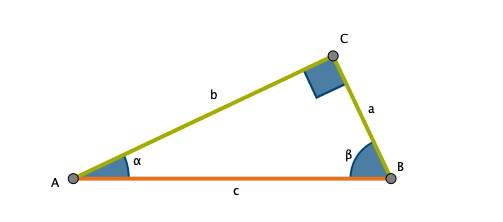
Der Sinus beschreibt das Verhältnis von Gegenkathete zur Hypotenuse, der Cosinus das Verhältnis der Ankathete zur Hypotenuse. Also:
\[\sin(\alpha)=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos(\alpha)=\frac{\text{Ankathete}}{\text{Hypotenuse}}\]
Durch die Benennung der Seiten mit $a, b$ und $c$ bekommen wir die Gleichungen:
\[\sin(\alpha)=\frac{a}{c}=\cos(\beta)\]
\[\cos(\alpha)=\frac{b}{c}=\sin(\beta)\]
Dreiecke mit einem rechten Winkel und einem weiteren gleich großen Winkel sind ähnlich zueinander. Somit bleibt das Verhältnis jeweils gleich.
Spitze Winkel
Durch die Winkelsumme im Dreieck von $180^\circ$ und dem rechten Winkel müssen $\alpha + \beta =90^\circ$ ergeben. Im rechtwinkligen Dreieck sind – vom rechten Winkel selbst abgesehen – folglich nur spitze Winkel zwischen $0^\circ$ und $90^\circ$ möglich. Mithilfe des Einheitskreises kann man Sinus und Cosinus auch für andere Winkel definieren beziehungsweise sich erschließen.
Weitere Informationen zu den trigonometrischen Funktionen finden sie in (Korntreff, 2017).